Lesson Five Topics

Lesson Five Overview
History of the Neutron Star
The Discovery of the Pulsar
Pulsars and Neutron Stars
How Do Neutron Stars Form?
Properties of Neutron Stars
The Magnetic Field of Neutron Stars
Why Do Neutron Stars Pulse?
Millisecond Pulsars
Pulsar in the Crab Supernova Remnant
Why Study Pulsars?

	Activities and Quizzes

Lesson Five : Activities and Quizzes

Activity 3: Neutron Stars

Materials: A pencil, a sheet of paper, and a calculator.

Procedure: Escape speed is the speed at which you would have to be traveling in order to escape the gravitational field of a celestial body. For instance, in order to escape the gravitational pull of Earth, the space shuttle must travel faster than 11,200 m/s.

Derived from the laws of motion discovered by Sir Isaac Newton, the equation used to calculate escape speed is



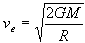
Where v_e is escape speed in meters per second, G is the gravitational constant (6.67 x 10^-11N*m³/kg*s²), M is the mass of the celestial object (i.e. Earth or the neutron star) in kilograms, and R is the radius of the celestial object in meters.

Notice that the mass of the object trying to escape the gravitational field is irrelevant in this equation. A 91.7 kg alien spaceship and a 6350 kg NASA shuttle would both have to travel over 11,200 m/s to escape Earth's gravity.

Calculations: Using a calculator and 3 significant digits, answer the following questions.

1. Calculate the escape speed of the moon, with a mass of 7.35 × 10²² kg and a radius of 1.74 x 10⁶ m.
2. Calculate the escape speed of our sun, with a mass of 1.92 × 10³⁰ kg and a radius of 6.95 x 10⁸ m.
3. Assume that you are exploring a neutron star with a mass of 1.99 × 10³⁰ kg (which is the mass of our sun) and a radius of 10,000 m. How fast do you have to go to escape the gravity of a neutron star?

Because of the extreme gravitational conditions on a neutron star, you cannot calculate the escape speed using Newton’s equations. In Newton’s times, he was unaware of the existence of these extreme conditions and his classical mechanics only apply to non-extreme objects. We can now calculate the escape speed on a neutron star using Einstein's theory of general relativity. Nonetheless, the calculation above will give you a rough idea of the tremendous speed required to escape the surface of a neutron star.

Solution